안녕하세요. 미분과 적분은 수학에서 중요한 개념인데, 뉴턴 역학과 연결되면서 물리 세계를 이해하는 데 큰 역할을 해요. 저도 처음엔 미분과 적분이 어렵게 느껴졌지만, 뉴턴 역학을 공부하면서 그 연결고리가 재밌어졌습니다. 이번 글에서는 "미분과 적분, 뉴턴 역학까지" 간단히 풀어볼게요. 미분과 적분을 쉽게 이해하고 싶은 여러분께 도움이 되길 바랍니다!

목차
1. 미분과 적분이란 무엇일까?
미분과 적분은 미적분학의 핵심이에요. 미분은 함수의 변화율을 구하는 방법이고, 적분은 변화량의 총합을 계산하는 도구입니다.
쉽게 말하면, 미분은 속도를 알아내고, 적분은 거리를 구하는 과정이라고 생각하면 돼요. 저는 처음 배울 때 이 개념이 추상적으로 느껴졌는데, 물리와 연결되니 훨씬 명확해졌어요.
Khan Academy에 따르면, 미분과 적분은 뉴턴과 라이프니츠가 역학 연구 중 발전시켰다고 합니다(Khan Academy).
2. 미분 쉽게 이해하기
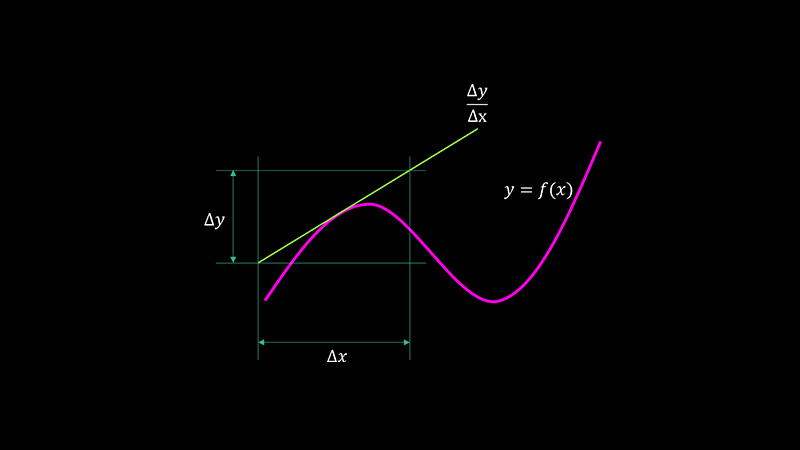
미분은 함수의 기울기를 구하는 거예요.
예를 들어, \( f(x) = x^2 \)의 미분은 \( f'(x) = 2x \)로, 각 점에서의 변화율을 알려줍니다.
\( f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \)
이 공식은 \( x \)에서 \( x+h \)로 갈 때의 평균 변화율이 \( h \)가 0에 가까워지며 순간 변화율이 되는 과정이에요.
저는 이 공식을 처음 봤을 때 복잡했지만, 그래프의 기울기로 생각하니 이해가 됐어요.
예를 들어, \( x = 2 \)일 때 \( f'(2) = 4 \)로 기울기가 4라는 뜻이죠.

3. 적분 쉽게 이해하기
적분은 미분의 반대 개념이에요. 함수의 면적이나 변화량의 총합을 구합니다.
예를 들어, \( f(x) = 2x \)의 적분은 \( F(x) = x^2 + C \)로, 면적을 구하거나 변화량을 계산해요.
\( \int_a^b f(x) \, dx \)
이건 \( a \)부터 \( b \)까지의 면적을 뜻하고, \( C \)는 상수예요.
저는 적분을 처음 배울 때 면적 개념이 생소했는데, 그래프 아래 영역으로 생각하니 훨씬 쉬웠어요.
4. 미분과 적분의 관계
미분과 적분은 서로 반대되는 관계예요.
미분한 함수를 적분하면 원래 함수로 돌아오고, 적분한 함수를 미분하면 원래 변화율이 됩니다.
이를 ‘미적분학의 기본 정리’라고 해요.
\( \int f'(x) \, dx = f(x) + C \)
\( \frac{d}{dx} \int f(x) \, dx = f(x) \)
저는 이 상호작용을 알게 되면서 미분과 적분이 하나로 연결된다는 걸 느꼈어요.

5. 뉴턴 역학과 미분 연결
미분은 뉴턴 역학에서 속도와 가속도를 구할 때 쓰여요.
예를 들어, 위치 함수 \( s(t) = t^2 \)가 있으면, 속도는 미분으로 \( v(t) = \frac{ds}{dt} = 2t \)입니다.
가속도는 속도의 미분, 즉 \( a(t) = \frac{dv}{dt} = 2 \)가 됩니다.
Newton’s laws에 따르면, 가속도는 힘과 질량의 관계를 나타내죠.
저는 물체의 움직임을 계산하며 미분이 얼마나 실용적인지 알게 됐어요.
6. 뉴턴 역학과 적분 연결
적분은 뉴턴 역학에서 속도로 거리를, 가속도로 속도를 구할 때 필요해요.
예를 들어, 가속도 \( a(t) = 2 \)가 주어지면, 속도는 적분으로 \( v(t) = \int 2 \, dt = 2t + C_1 \)입니다.
위치는 속도의 적분, 즉 \( s(t) = \int (2t + C_1) \, dt = t^2 + C_1 t + C_2 \)가 됩니다.
저는 이 과정을 풀어보며 적분이 움직임의 총량을 계산한다는 걸 이해했어요.
7. 예제 풀이: 속도에서 거리 구하기
예제를 풀어볼게요.
문제: "속도 \( v(t) = 3t \)일 때, 0초부터 2초까지의 거리는?"
거리는 속도의 적분이에요.
\( s(t) = \int 3t \, dt = \frac{3}{2} t^2 + C \)
0초에서 2초 구간의 거리는 \( s(2) - s(0) = \frac{3}{2} (2)^2 - \frac{3}{2} (0)^2 = 6 \)입니다.
저는 이 문제를 풀며 적분이 실생활 움직임을 계산하는 데 유용하다는 걸 알았어요.
8. 미분과 적분 활용 팁
미분과 적분을 쉽게 쓰려면 기본 개념을 익히는 게 중요하며 미분은 변화율, 적분은 누적량으로 생각하세요.
문제 풀 때 공식을 먼저 떠올리고, 간단한 예제로 연습하면 실수가 줄어듭니다.
저는 속도와 거리 문제를 풀며 개념이 명확해졌어요.
이상으로 미분과 적분, 뉴턴 역학까지의 연결을 정리해봤습니다. 저는 이 과정을 공부하며 수학과 물리가 이렇게 맞물리는 게 신기했어요. 여러분도 미분과 적분을 쉽게 이해하고, 뉴턴 역학 문제로 실력을 키워보시길 바랍니다.
'생활정보 > 교육정보' 카테고리의 다른 글
| 밀도 구하는 공식(ρ=m/V), 개념 잡는 쉬운 설명 (0) | 2025.02.27 |
|---|---|
| 속력 구하는 공식(v=d/t), 문제 풀이로 익히기 (0) | 2025.02.27 |
| 등차수열의 합 공식, 공식 유도부터 문제 풀이까지 (0) | 2025.02.26 |
| 삼각형 높이 구하는 방법 쉽게 이해하기 (0) | 2025.02.17 |
| 피타고라스의 정리 개념과 증명 쉽게 이해하기 (0) | 2025.02.16 |



